8.メッシュ分割
応力集中部や板厚方向のメッシュ分割は計算精度に大きく影響する。
小さい要素にすれば計算精度は上がるが、実際にはPCで計算できないようなモデルの規模(節点数)になってしまうことがよくある。
そこで要素分割と精度の関係をある程度把握した上でメッシュ分割をする必要がある。
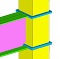
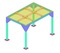
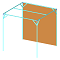
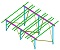
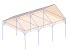
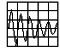
下図構造の1/4モデルに対し、メッシュ分割をN=2、4、6、8、16、24、32とした時の応力変化を確認する。
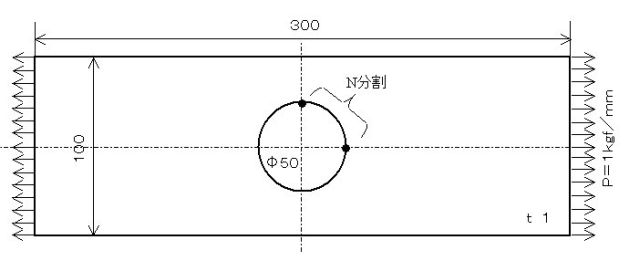
最大の集中応力σmaxは、メッシュ分割がどの場合でも、矢印の点だった。
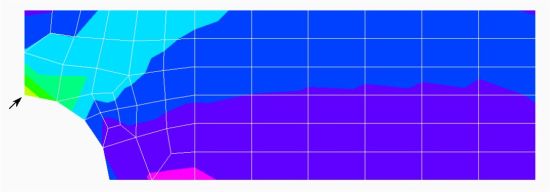 |
 |
| N=4、σmax=3.465461 | |
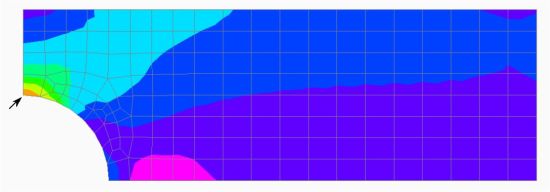 |
|
| N=8、σmax=3.983835 | |
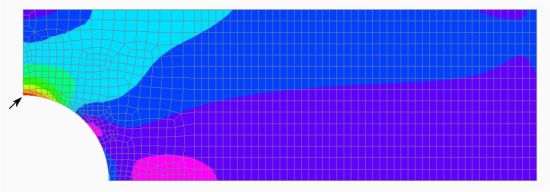 |
|
| N=32、σmax=4.307712 |
この、Nとσmaxの関係をグラフで表すと、
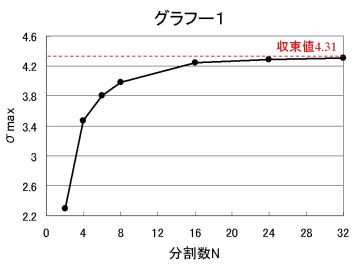
となり、Nが増すと、σmaxは4.31収束していくことがわかる。
また、応力集中の程度は、応力集中係数αkで表すことができ、下図の式となる。

αkは、鵜戸口英善著『材料力学 下巻』裳華房発行の下図グラフに、N=32の時の解析データ(αk=2.153856)をプロットしてみるとよく一致していることがわかる。
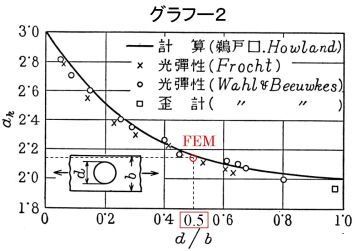
グラフ-1の結果から、実際の解析において穴まわりの分割数を4程度にすれば、誤差は20%で、実用上問題ないと考えられる。