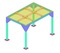
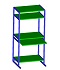
構造計算と構造解析の違い
建築設計のいわゆる”構造計算書”や機械設計の”設計計算書(強度計算書)”では材料力学の梁理論の公式などをそのまま適用するため、計算できるのは単純な構造に限定され、細部の応力は分かりません。一方、構造解析は有限要素法(構造体を単純な形状の要素の集合体と考える)を使用するので、複雑な三次元の構造も計算可能で、細部の応力も確認できます。
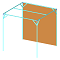
従来の構造計算(強度計算)
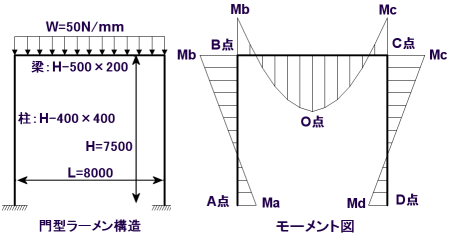
梁の柱に対する剛比k=Kbc/Kab=(Iab/H)/(Ibc/L)=0.659
曲げモーメント:Ma=Md=WL^2/(12*(2+k))=1.003×10^8 N・mm
Mb=Mc=-WL^2/(6*(2+k))=2.006×10^8 N・mm、
Mo=WL^2*(2+3k)/(24*(2+k))=1.994×10^8 N・mm
断面係数:Zab=3.33×10^6 mm^3、Zbc=1.87×10^6 mm^3
柱の最大曲げ応力(B、C点位置)=σab=Mb/Zab=60 N/mm^2 = 60 MPa
梁中央の曲げ応力(O点位置)=σbc=Mo/Zbc=107 N/mm^2 =107 MPa
∴門型ラーメン構造の最大応力 = 107 MPa(梁中央)
構造計算では複雑な応力分布は分からない
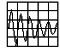
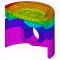
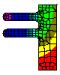
構造解析による計算(弊社の方法)
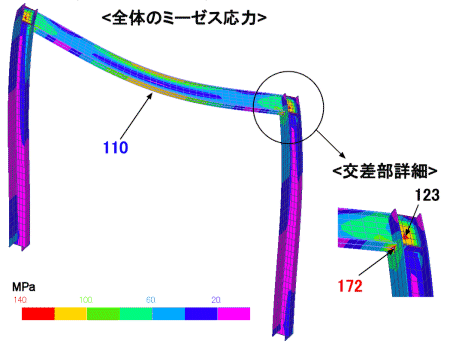
梁中央の応力は下記の構造計算とほぼ一致していますが、計算式を当てはめ難い交差部には応力集中による最大応力が発生しています。
構造解析では詳細な応力状態も確認可能